ssssecret

I want to share a secret,
A secret dear to me.
But the secret to keeping a secret
Is to never give out the key.

So I broke it up in little pieces
As small as they can be.
Then after that you wouldn’t expect
I handed them out for free.

Follow up these pieces
Understand them to a degree
At the very root of it all
The answer you will see

AES-ECB(‘6eeb7683e9242ed56080e847c2f94cfc50634c29a3a50f14b31e7e3f97e34df0’, key)

(1, d8877abe8c795a869b1fe28ed9a328a4)
(2, 1a1c134fc5c474899ee9d573b8895388)
(3, da143ab7a656e69a91b22414de846d0e)
(4, e4c6d40f50bd5f37d5c2f5e356a0af94)
(5, f344401d9a20a8ea1f08598434bfbf8e)

As soon as I saw this, I immediately recognized what this challenge was about; Shamir’s Secret Sharing Scheme.

This scheme can turn a secret into n “parts”, relying on a simple trick.

The essential idea of Adi Shamir’s threshold scheme is that 2 points are sufficient to define a line, 3 points are sufficient to define a parabola, 4 points to define a cubic curve and so forth. That is, it takes k points to define a polynomial of degree k - 1.

What the heck?

In a nutshell, what this is saying is that in order to recover the secret, all the parts are needed (or some of the parts, determined by the threshold, but let’s not complicate things). The reason this works is that if you have a polynomial with 5 terms (such as this challenge), if you don’t know all 5 coefficients, there is no way to reconstruct the polynomial, even if you have some of the parts, as there are an infinite number of solutions for them.

If you want to find out how this works exactly, I can recommend just skimming through the wikipedia page.

Getting back the secret

Thankfully, we know all parts needed to get the secret back for this challenge. I used ssss-combine from point-at-infinity.org/ssss.

At first, the tool did not work and gave me back a wrong result, so initially I skipped this challenge, but it kept bugging me that I knew the solution, but the tooling just didn’t seem to work.

As it turns out, for whatever reason, I needed to give ssss-combine the -D flag so that it works, I have no idea why that is needed, but oh well, you can’t know everything.

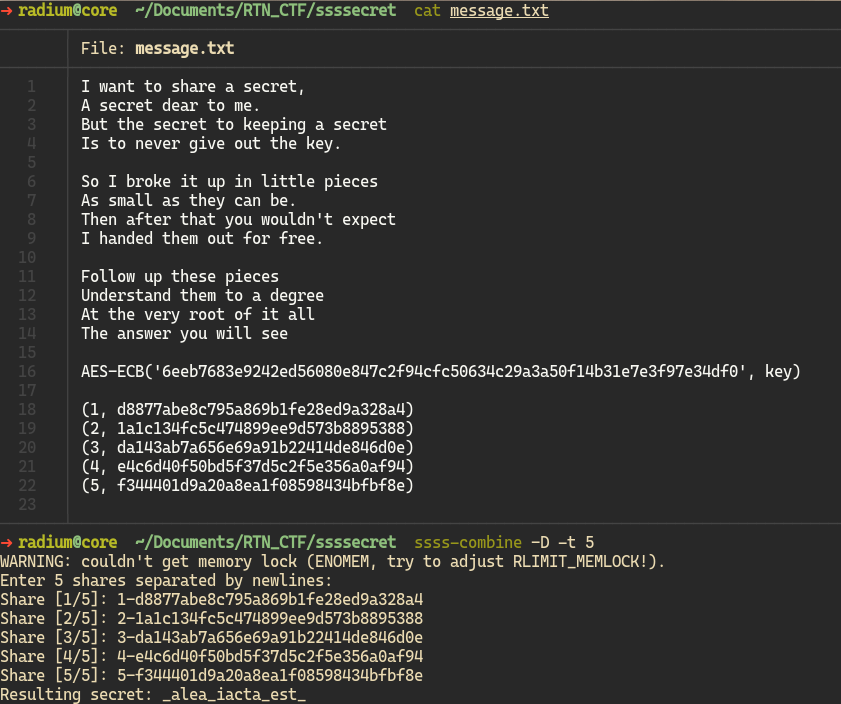
Fun fact: The secret (“Alea iacta est”) means “The die has been cast” in English.

Decrypting the message

Now that we have the secret, we just need to decrypt the ciphertext with AES in ECB mode, but there is a problem. Where is the IV?!

After some googling, I found out that ECB mode employs no IV, so all we have to do is just decrypt the ciphertext without an IV! Cyberchef to the rescue!

With the following settings we get our flag at last: RTN{ssso_v4ry_s3cr3t}.